Hardness Conversion
STEEL HARDNESS CONVERSION
Approximate equivalents between the Brinell and Rockwell hardness scales, as well as their rough correlation to material tensile strength.
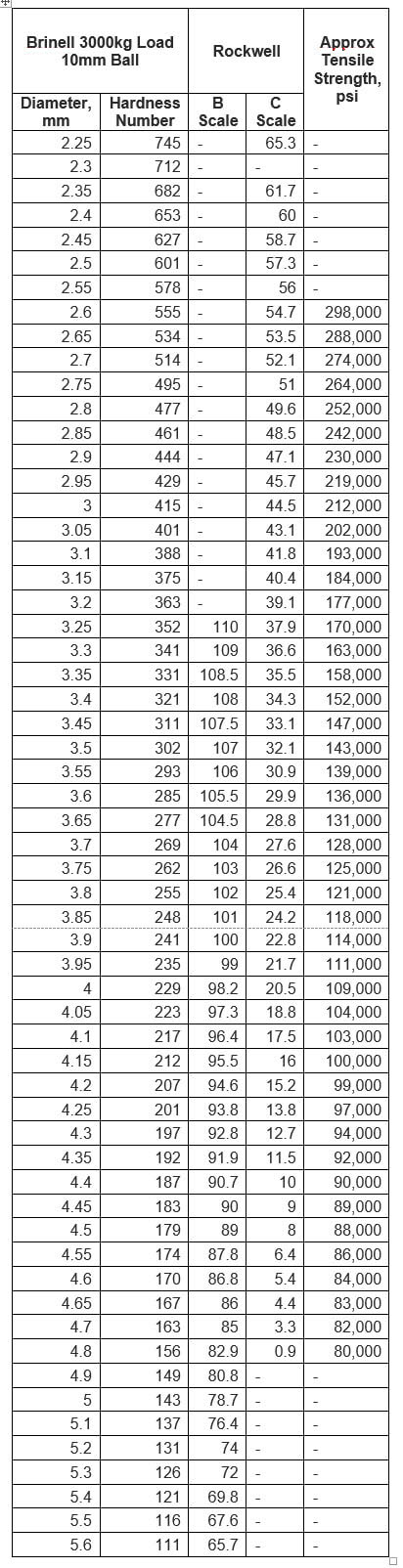
Hardness testing of steel is typically done on one of two scales, Rockwell or Brinell. These two scales are similar and each has equivalents on the other scale, similar to the relationship between Celsius and Fahrenheit. They differ in their testing methodology, but both are indentation hardness scales, operating on the principle that material tensile strength is directly correlated to the amount a hardened ball (or cone) will penetrate.
Rockwell
There are seven separate scales under the Rockwell umbrella, letters A-G, but the most common scales used on steel are B and C, often abbreviated HRB and HRC respectively. The B scale is typically used on softer steels, those under approximately 115,000psi tensile. Testing on the B scale involves a 1/16” steel sphere and a load of 100kgf. The testing machines then determine the amount of indention and assign it a hardness number, example 98 HRB. Readings above 100 HRB are generally considered unreliable, so the C scale is then used. The C scale is typically used on harder steels, like those above about 110,000psi tensile. Testing on the C scale involves a 120° diamond cone and a load of 150kgf. The test is carried out the same way as the B scale test above, and the result is written as 28 HRC. Readings below 20 HRC are generally considered unreliable, so the B scale is used.
Brinell
The Brinell hardness testing method is similar to the above Rockwell testing method with a couple differences. A typical test on steel uses a 10mm diameter steel (or tungsten) ball with 3,000kg of force. A steel ball is used for most materials; the tungsten ball is used primarily for harder materials like tool steel. When a steel ball is used, the result is written as BHN or HBN, example 285 HBN. When a tungsten ball is used, the result is written as HBW, W is the chemical symbol for tungsten (wolfram). Brinell testing is generally considered to be more accurate because the larger ball size makes deeper and wider indentations, thereby averaging the test out over a wider amount of material. However, due to the larger nature of the indentations, it is often considered a destructive test.